Category Trend  Published on 16/08/2023

Hanning (FIR) Filter

Subscribe
An update for this algorithm is currently pending moderation. Please revisit this page shortly to access the algorithm's latest version.
Description

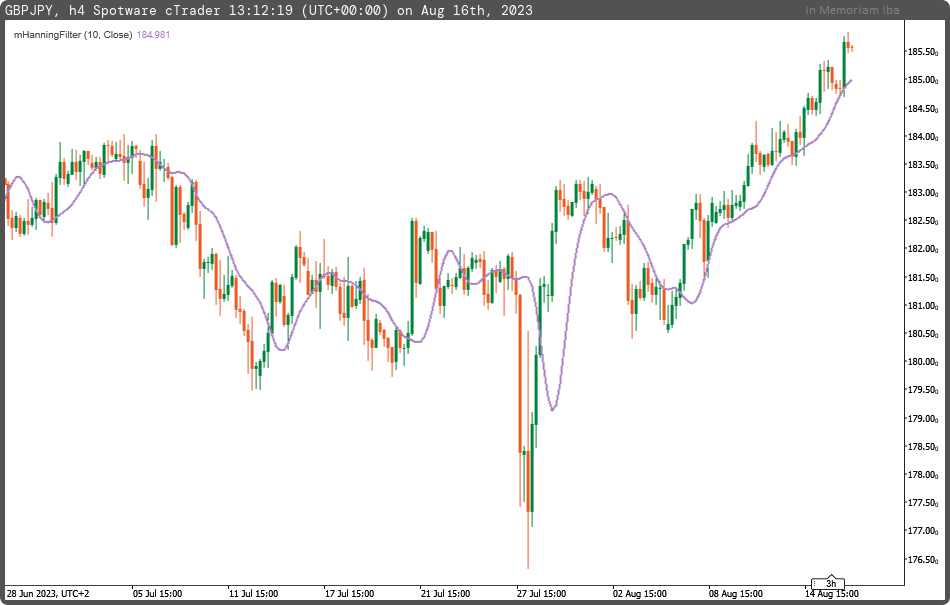
Hanning FIR Filter

The Hanning Finite Impulse Response (FIR) Filter is a fundamental digital signal processing tool used to manipulate and enhance signals in various applications. As an end user, understanding the basic concepts of the Hanning FIR Filter can help you make informed decisions when working with digital signal processing tasks.

What is the Hanning FIR Filter?

The Hanning FIR Filter is a type of digital filter used to modify the characteristics of a signal. It falls under the category of Finite Impulse Response filters, which means its output is determined by a finite number of input samples.

Key Characteristics:

Window Function: The Hanning FIR Filter uses a Hanning window function, also known as the Hann window or raised cosine window, to shape the impulse response of the filter. This windowing technique helps mitigate the issue of spectral leakage in frequency analysis.

Frequency Response: The filter's frequency response exhibits a main lobe with lower side lobes. This characteristic makes the Hanning FIR Filter useful for applications where attenuation of side lobes is important.

Passband and Stopband: The Hanning FIR Filter is designed to pass certain frequency components (passband) while attenuating others (stopband), according to the desired filter specifications.

User Benefits:

Improved Signal Quality: By applying the Hanning FIR Filter, you can enhance the quality of a signal by removing unwanted noise or unwanted frequency components.

Frequency Analysis: The Hanning FIR Filter can be used to isolate specific frequency ranges of a signal, aiding in tasks such as signal separation and analysis.

Customizable Design: As an end user, you can adjust the filter parameters to tailor its behavior according to your specific signal processing requirements.

Limitations:

Finite Impulse Response: The Hanning FIR Filter has a finite memory, which means its ability to capture long-duration effects in a signal is limited compared to Infinite Impulse Response (IIR) filters.

Design Complexity: Designing an optimal Hanning FIR Filter requires some understanding of filter design principles, including trade-offs between filter order, passband ripple, and stopband attenuation.

Applications:

Audio Processing: The Hanning FIR Filter is used in audio applications to remove noise, enhance speech clarity, and create audio effects.

Image Processing: In image processing, the filter can be employed for edge enhancement and noise reduction.

Communication Systems: The Hanning FIR Filter helps in improving the quality of transmitted signals and reducing interference in communication systems.

Conclusion:

In conclusion, the Hanning FIR Filter is a valuable tool in the realm of digital signal processing. As an end user, understanding its basic principles, characteristics, and applications can empower you to effectively manipulate and improve signals in various domains.
mfejza's avatar
mfejza

Joined on 25.01.2022

  • Distribution: Free
  • Language: C#
  • Trading platform: cTrader Automate
  • File name: mHanningFilter.algo
  • Rating: 5
  • Installs: 462
  • Modified: 16/08/2023 13:20

Download
Comments
Log in to add a comment.
mfejza's avatar
mfejza · 1 year ago 
using System;
using cAlgo.API;
using cAlgo.API.Indicators;
using cAlgo.API.Internals;

namespace cAlgo
{
    [Levels(0)]
    [Indicator(IsOverlay = true, TimeZone = TimeZones.UTC, AccessRights = AccessRights.None)]
    public class mHanningFilter : Indicator
    {
        [Parameter("Period (10)", DefaultValue = 10, MinValue = 3)]
        public int inpPeriod { get; set; }
        [Parameter("Data Source (close)", DefaultValue = enumPriceTypes.Close)]
        public enumPriceTypes inpPriceType { get; set; }    

        [Output("Hanning Filter", LineColor = "FFAA83C6", PlotType = PlotType.Line, LineStyle = LineStyle.Solid, Thickness = 2)]
        public IndicatorDataSeries outHanningFilter { get; set; }
        
        private IndicatorDataSeries _price, _filt, _hanningfilter;
        private double _coef;
        

        protected override void Initialize()
        {
            _price = CreateDataSeries();
            _filt = CreateDataSeries();
            _hanningfilter = CreateDataSeries();
            for (int j=1; j<inpPeriod; j++)
                _coef += (1 - Math.Cos(2.0 * 3.1415926 * j / (inpPeriod + 1)));
        }

        public override void Calculate(int i)
        {
            switch(inpPriceType)
            {
                case enumPriceTypes.Open:
                    _price[i] = Bars.OpenPrices[i];
                    break;
                case enumPriceTypes.Close:
                    _price[i] = Bars.ClosePrices[i];
                    break;
                case enumPriceTypes.High:
                    _price[i] = Bars.HighPrices[i];
                    break;
                case enumPriceTypes.Low:
                    _price[i] = Bars.LowPrices[i];
                    break;
                case enumPriceTypes.Median:
                    _price[i] = Bars.MedianPrices[i];
                    break;
                case enumPriceTypes.Typical:
                    _price[i] = Bars.TypicalPrices[i];
                    break;
                case enumPriceTypes.Weighted:
                    _price[i] = Bars.WeightedPrices[i];
                    break;
                default:
                    _price[i] = Bars.ClosePrices[i];
                    break;
            }
            
            _filt[i] = 0;
            for (int j=1; j<inpPeriod; j++)
                _filt[i] += (1 - Math.Cos(2.0 * 3.1415926 * j / (inpPeriod + 1))) * (i>inpPeriod ? _price[i-j-1] : _price[i]);
            _hanningfilter[i] = _coef!=0 ? (_filt[i] / _coef) : _filt[i];
            
            outHanningFilter[i] = _hanningfilter[i];
        }
    }
    
    public enum enumPriceTypes
    {
        Open,
        Close,
        High,
        Low,
        Median,
        Typical,
        Weighted
    }
}
 
Copyright © 2024 Spotware Systems Ltd. All rights reserved.
cTrader Ltd offers through its group of companies the cTrader platform. The information on this website is for general informational purposes only and does not constitute financial or investment advice. cTrader does not solicit retail investors. Reliance on this information is at your own risk.